Light Travels Through a Substance at 1.97
Refraction of waves leads to many familiar phenomena
Refraction of light leads to many phenomena you've probably seen, and some that are very useful in science, engineering science, and sometimes fine art.
The bones idea is that light does not travel at the same speed in all transparent materials. For example, the speed of calorie-free in vacuum is
$$c = ii.99792458 \times 10^viii \, \frac{m}{south},$$
only information technology slows, for case, to one.97 × ten8 m/s in common window glass.
In diamond, the speed of light is about 1/3 of its speed in vacuum, and this in office leads to the sparkle and color of high-quality diamonds.
The essence of refraction is this speed departure in dissimilar materials. When light beams pass from one textile to another, in which the speed of calorie-free is different, its path bends at the interface.
Refraction is responsible for the separation of colors in a prism, the mirage "lakes" you see at the end of a hot road in summer, the midday sky being blue and the forenoon and evening skies being orange and cherry-red.

We'll see how it all works in this section. First nosotros'll define the index of refraction for convenience, then we'll employ Snell's constabulary to calculate refraction angles.
A derivation of Snell's law is given at the end of this section, but you'll need to know most differential calculus to follow it. Don't worry about it if you haven't studied calculus yet. Just utilise the law and come back to how it's derived later.
X
Interface
An interface is a line or surface that separates two types of material.
The surface betwixt air and water is an interface. Then is the surface between the oil and h2o when oil floats on top of h2o.
The index of refraction, north
The index of refraction ( due north ) of any material is the ratio of the speed of calorie-free in vacuum, $c = 2.99792458 \times 10^viii \, m/s,$ to the speed of light in that material.
$$north = \frac{c}{v}$$
where v is the speed of light in the material. Notice that because we divide a velocity by a velocity hither, the result is unitless.
The index of refraction, $n,$ is unitless.
Calorie-free travels its fastest in vacuum, and slows downward in all other materials, and then the index of refraction of materials is always a number greater than 1. The larger the index of refraction, the smaller the speed of low-cal in the fabric. In other words, north is inversely proportional to the speed of light in the detail textile.
The table shows the speed of light and index of refraction for several transparent materials.
The index of refraction can be measured for materials that aren't transparent to visible lite (opaque materials) by using loftier energy radiation that penetrates such materials, such as gamma rays.
Speed of lite and index of refraction (northward) in various transparent materials
| medium | speed (yard/s) | n |
|---|---|---|
| vacuum | two.9979 × 10viii | 1.00 |
| air | 2.9970 × x8 | 1.0003 |
| h2o | two.25 × 108 | 1.33 |
| ethanol | 2.20 × 108 | ane.36 |
| quartz | 2.0555 × 10eight | 1.4585 |
| window glass | 1.97 × 108 | 1.52 |
| diamond | 1.24 × teneight | 2.42 |
Snell'due south police force*
Snell'due south law allows us to chronicle the angle of incidence and the angle of refraction to the indices of refraction, n1 and north2 .
The effigy shows a beam of light entering water from air at an angle from the vertical. The figure shows that the angles of incidence ( θi ) and refraction ( θr ) are divers with respect to the normal to the interface. A normal is a line that is perpendicular to an interface from all angles with respect to the interface surface.
Snell'due south law is
$$n_1 \, sin(\theta_1) = n_2 \, sin(\theta_2)$$
We tin can rearrange Snell's police force to solve for the bending of refraction, θtwo , using some inverse trigonometry:
$$ \brainstorm{align} n_1 \, sin(\theta_1) &= n_2 \, sin(\theta_2) \\[5pt] \frac{n_1 \, sin(\theta_1)}{n_2} &= sin(\theta_2) \\[5pt] \theta_2 &= sin^{-one} \left( \frac{n_1 \, sin(\theta_1)}{n_2} \correct) \end{align}$$
At present if our beam of lite passes from a medium with a higher speed of calorie-free (smaller northward) into one with a lower speed (larger due north), then n1/north2 ≤ ane. It's also true that θ ≤ π/2 because we won't have an angle of incidence greater than or equal to a right bending (beam skimming along the surface but not inbound). Farther, because the sine function betwixt 0 and π/two is an increasing role with a maximum of 1 at θ = π/2, the sine of a larger angle is larger than the sine of a smaller angle. Rearranging Snell's law another manner gives:
$$\frac{n_1}{n_2} \ \frac{sin(\theta_2)}{sin(\theta_1)}$$
This means that for low-cal passing from a medium of low refractive index to a higher alphabetize, the angle with respect to the normal will decrease. The opposite must be truthful for light moving from a higher alphabetize to a lower i.
The diagram shows this situation for low-cal passing from air to a liquid. The incident beam is measured from the normal to the interface, and the angle that the refracted axle makes with that same normal will be smaller.
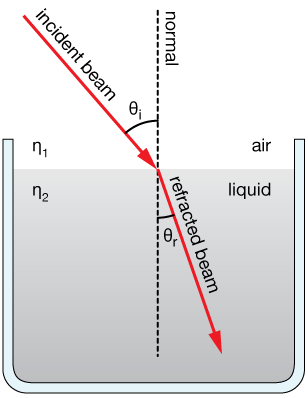
This state of affairs can be reversed. If the beam originates in the liquid (larger n) and passes through to air, the angle fabricated with the interface normal will increase. In the examples below we tin go quantitative about information technology.
* Snell's law is derived using calculus at the bottom of the page.
Snell'due south law
When lite passes through an interface separating two media in which the speed of light (and thus the index of refraction, n) is different, the angle of that calorie-free with respect to the normal to the interface will change according to Snell'south law:
$$n_1 \, sin(\theta_1) = n_2 \, sin(\theta_2)$$
where ni and north2 are the indices of refraction in medium ane & 2, respectively, and θ1 & θ2 are the angle fabricated past the beam of calorie-free and the normal to the interface between the ii media.
Direction of refraction
When light enters a medium with a higher index of refraction, its bending with the normal to the interface will decrease.
When light enters a medium with a lower alphabetize of refraction, its angle with the normal to the interface volition increase.
Example one
A beam of light passes into a flat slice of glass at an bending of 50˚ with respect to the surface normal. Calculate the angle of the refracted beam within the glass and after information technology passes through the other side back into air.
$$\theta_{r1} = sin^{-i} \left( \frac{n_{air} \, sin(\theta_{i1})}{n_{drinking glass}} \right)$$
If nosotros plug in nair = 1.00, θ1i = 50˚ and northdrinking glass = 1.52 (from the table above), we get
$$\theta_{r1} = sin^{-ane} \left( \frac{i.00 \, sin(l˚)}{1.52} \right)$$
and θr1 is, as expected, less than 50˚:
$$\theta_{r1} = xxx.3˚$$
Now to solve for the exit angle at the other interface, nosotros have to describe a new surface normal (shown as "normal-ii"). The bending of incidence with respet to that normal is just the bending of refraction of our offset beam, 30.3˚, and we'll name it θ2i , the "2d angle of incidence," simply to continue things organized.
Snell's law gives usa the formula for our exit angle:
$$\theta_{r2} = sin^{-1} \left( \frac{n_{glass} \, sin(\theta_{i2})}{n_{air}} \right)$$
Plugging in the numbers gives the states an easy expression to calculate (brand sure your calculator is set up to degrees!)
$$\theta_{r2} = sin^{-1} \left( \frac{one.53 \, sin(30.3˚)}{1.00} \right)$$
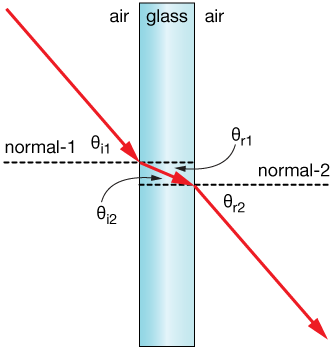
The exit angle turns out to exist the same equally the entrance angle,
$$\theta_{r2} = fifty˚$$
That'south the way it is for beams entering flat panes of drinking glass. The prototype is shifted a chip, but the archway and leave angles volition exist the same. Whenever you look at an image non at ninety˚ to a window, you're really seeing it shifted slightly to the left or right. You might get some roundoff fault in calculations like this using the sine role, but if you keep enough digits in your intermediate calculations, the approachable bending should match the incoming angle.
Example 2
A beam of light passes into a prism, a piece of glass with the cross-section of an equilateral triangle, such that it enters one side parallel to the base. Calculate the total angle of angle of this beam every bit it passes through the prism.

With xxx˚ as our first bending of incidence, we tin can summate the angle of the beam from the normal within the drinking glass. Snell's law, rearranged to solve for the angle of refraction, is
$$\theta_r = sin^{-1} \left( \frac{n_{air} \, sin(\theta_i)}{n_{glass}} \right)$$
Plugging in the the angle and the indices of refraction gives united states
$$\theta_r = sin^{-1} \left( \frac{1.00 \, sin(30˚)}{1.52} \right)$$
So the kickoff refraction angle, with respect to the surface normal on the left side of the prism, is
$$\theta_r = nineteen.205˚$$
At present the two surface normals in the diagram above must meet at a 120˚ angle, and if the angle of refraction of the incoming axle is 19.205˚, and then 180˚ - xix.205˚ gives united states of america the bending of incidence with the correct-side surface normal, θi = 40.795˚.
In the same way as nosotros did for the starting time angle, we can now solve for the second angle of refraction, as the axle emerges from drinking glass into air:
$$\theta_r = sin{-i} \left( \frac{n_{glass} \, sin(\theta_i)}{n_{air}} \right)$$
Plugging in the angle and the indices of refraction gives
$$\theta_r = sin{-1} \left( \frac{1.53 \, sin(40.795˚)}{1.00} \right)$$
which gives united states of america the concluding angle of refraction.
$$\theta_r = 89˚$$
Here'south the diagram with all of the angles:
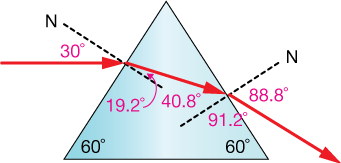
The supplementary angle to 88.8˚ is 91.2˚, and if nosotros decrease 30˚ from that we get an overall downward bending from the initial beam striking the prism of 61.2˚.
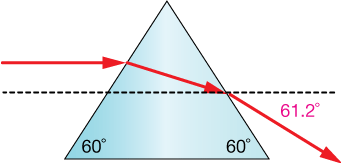
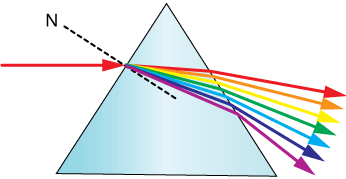
The geometry of the prism leads to large overall angle of the beam. Because the colors of white light bend differently (meet below), the prism shape is ideal for separating those colors by refraction.
Wavelength dependence of refraction
A prism is not only a terrific refractor of visible light, but it is as well capable of separating that calorie-free into individual color "bands." You lot accept probably seen the familiar rainbow of colors dispersed when white calorie-free (such as sunlight) passes through a prism.
Apparently, in that location is some dependence the amount of refraction on the wavelength of the light. It's actually on the refractive index of the fabric. Here's how that works: Kickoff, we know that the index of refraction of a transparent material is the ratio of the speed of light in vacuum to the speed of light in the cloth:
$$n = \frac{c}{5}$$
At present c is the speed of low-cal in vacuum, and we'll ready it equal to λo νo , the wavelength and frequency of the calorie-free in vacuum. Besides, the speed of light in the material is five = λ νo , Hither I've put the frequencies (Greek letter nu) in carmine to distinguish them from the velocity v.
$$c = \lambda_o \, \color{#E90F89}{\nu_o} \phantom{00000} v = \lambda \, \color{#E90F89}{\nu_o}$$
The key is that as low-cal passes through a medium other than vacuum, its frequency doesn't change, merely its wavelength. The spacing in time between peaks of an EM moving ridge entering and passing through a medium is constant, only because of the alter in speed, the spacing between those peaks, λ, is different. Here's a little animation that might help to illustrate the phenomenon. A wavefront with a certain wavelength passes through a medium (blueish box) in which the speed is almost 65% of the speed exterior it.
You lot tin can see that the waves "stack up" a trivial tighter as they pass through the box, and then aggrandize again on the other side. Play the animation a few times until you see information technology clearly.
You might have noticed this same kind of affair if you're a skier. Detachable chair lifts practise the same sort of thing at the top and bottom of the elevator, where the chairs detach from the rope, slow and decrease spacing. The are spaced back out again when they reattach for the second function of the ride, but the number of chairs that laissez passer any point in a given time (frequency) is always the same.
Constant frequencies means that nosotros can cancel the frequencies in this new expression for the index of refraction:
$$ \require{cancel} n = \frac{\lambda_o \cancel{\nu_o}}{\lambda \cancel{\nu_o}}$$
Then we accept a formula for the index of refraction as a function of the wavelength of light, or the ratio of the wavelength in vacuum to the wavelength in the medium:
$$n = \frac{\lambda_o}{\lambda}$$
When the speed of light in a substance is lower than vacuum or air (very shut to vacuum), then the wavelength must exist reduced to produce that lower speed $(c = \lambda \, \nu).$
This ways that the alphabetize of refraction for long wavelengths is smaller than for shorter wavelengths. That matches our dispersed rainbow of colors from the prism: Red is the least-bent of the colors and violet the near.
Why the sky is blue
Daytime
The sky is not blue because it reflects the oceans. Distressing, not truthful.
The daytime heaven is bluish considering air has an alphabetize of refraction greater than 1 (though not much greater), and partially because that alphabetize changes with the temperature of the atmosphere.
Equally the diagram shows, at normal angles to the sun in daytime, colors in the blue stop of the spectrum are refracted near by the atmosphere, and tend to strike the surface where we live.
It'due south also true that at very high altitudes the heaven gets much darker, more than toward the red stop of the spectrum.
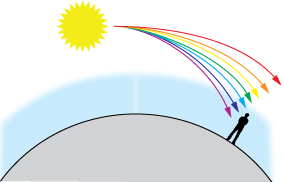
That makes sense if nosotros're climbing into the zone where cerise light, which normally passes loftier overhead, now is more visible.
Morning time and night
At sunrise and dusk we tend to see red-orange skies. That'southward because Earth and the sun are in a position that places the sun at or beneath the real horizon, the highest ground that can be seen past an observer looking toward the sunday.

Equally the diagram shows, the atmosphere is behaving in the aforementioned way as daytime, except that at present, because of the distance the rays travel through the atmosphere on their way to the observer, the rays on the violet/blueish end of the spectrum bend down and strike the planet well before striking the observer.
The rays on the red end of the spectrum, which are deflected less by the atmosphere, "survive" the trip to the observer, who sees mostly red and orange.
Mirages – seeing what's not there
Yous've probably been in a car on a hot twenty-four hours and noticed that at the end of a stretch of hot road, the roadway seems to exist wet, like there's a lake ahead. That's a mirage, and information technology's caused by the alter in refractive index between cool and warm air. Roll over or tap the desert image below to see the delusion lake at the cease of this hot desert flooring.

What's happening is that there is a difference betwixt the index of refraction of the cold air to a higher place the desert and the air simply above the hot sand, which radiates sunlight dorsum into the atmosphere. This hot air layer has a relatively big index of refraction and bends light from the mountains and sky directly to the eyes of an observer on the ground.
What the observer is seeing isn't a lake at all, it'due south just a patch of light from the heaven, the rays of which have been aptitude by refraction.

Lenses: convex
Nosotros can see how lenses piece of work merely using the bones rules of refraction. Nosotros'll practice information technology qualitatively here (without numbers) just to get the general features.
![]()
First consider the beam of light moving from the left side into the lens. An interface normal is drawn there. To draw a normal to a surface, nosotros first depict a tangent line (T) to the entrance point on the bend.
And so the normal (N) tin be drawn perpendicular to that. In reality, of course, that tangent line is a plane that is tangent to a 3-dimensional lens, simply this 2d representation will serve our purpose just fine.
At present Snell's law says that the angle made to the surface normal should decease in glass, which has a larger index of refraction (slower speed of light) than air. That smaller angle is drawn every bit the upper low-cal beam angles down through the lens.
Now equally that aforementioned beam exits the lens, the interface normal is tilted in the opposite direction. At this interface the index of refraction decreases, and so the angle between the beam and the interface normal increases, further bending the lite in the aforementioned direction. This arched lens (convex on both sides) is really a lot like the prism above, it simply doesn't bend the light then dramatically.
The management of this angle is opposite on the lower office of the lens, and beams passing through the center of the lens aren't bent at all.
A biconvex lens, or even a convex lens with 1 flat side (you tin practice the geometry on that one) serves to focus incoming light. That lite can exist focused to a point or any other shape if the lens is designed carefully enough.
Lenses: concave
A concave lens forms a pocket or cave on at least one side. shown hither is the cross section of a biconcave lens, with concave faces on both sides.
Concave lenses are used to spread out the beams of incoming lite. Commencement with the upper incoming beam on the left side. The angle information technology makes with the interface normal (which is perpendicular to the tangent line, T, at that point) is smaller inside the glass, where the index of refraction is smaller (speed of lite is slower).
And so equally the beam strikes the second interface, the normal has a nearly opposite angle (sloped down instead of upward in this figure) and as the low-cal bends abroad from the normal, information technology is further defocused.
A planar-concave lens does the same thing, only to a lesser caste. The geometry of that kind of lens is left for you to sketch out (try it!).
A combination of convex and concave lenses is used in devices similar microscopes and telescopes to provide potent magnification and still make an image that the human eye can focus.
![]()
Pro tip
To recall which lens is concave and which is convex, call up that a con-cave lens makes a cave shape.
Fermat's principle of least time
Pierre de Fermat (1601-1665), who contributed richly to physics and mathematics, proposed that the path of a beam of light through whatever medium of combination of media was the ane that took the least possible time. This is known as the principle of to the lowest degree time (also known as Fermat's principle).
Succintly, Fermat said that out of all possible paths between ane indicate and another, light takes the one that takes the to the lowest degree time.
While Fermat'due south principle doesn't really tell united states why light behaves in that mode in matter, it does requite us some foundation for rules like Snell's police force.
Fermat's principle is well suited for using techniques of differential calculus, particularly optimization using the derivative. That is illustrated in the derivation of Snell's law at the bottom of this folio.
Ane example of such a problem is this:
Imagine that you are on the beach and you spot someone offshore who looks to exist drowning (figure beneath). Y'all need to run and swim to reach that person, and information technology's of import that you do it in the least fourth dimension. Y'all could jump in the water where you are and swim the long diagonal path, but yous swim more than slowly than you lot run. You could run until the victim is perpendicular to the beach and you have to swim through the least-possible water, only that'south probably non the optimal (least time) path either. The optimal path is somewhere in betwixt.

Information technology's the aforementioned for light. Take a look at the diagram below. It shows calorie-free passing from air through two different transparent media (green and blue) with different indices of refraction, and and then dorsum into air. It'due south a sketch of light traveling from point A to betoken B through zones in which the speed is different (like your speed on sand and in water).
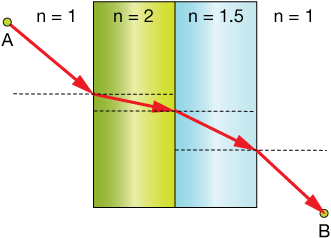
In the dark-green medium, the speed is slower (larger north), then the beam takes a more directly path through it (closer to perpendicular) to minimize the fourth dimension. Relative to the green zone, light travels faster through the blue medium, so information technology tin can bend and spend a picayune more time there before emerging and proceeding through B. That's the fastest path, and it'south faster than if we merely drew a direct beam from A to B.
Now if our axle had entered at a right angle to those to slabs of material, the fastest path through would have been a straight line. It changes when that first bending of incidence changes.
Derivation of Snell'southward law (calculus )
In this section nosotros show how to derive Snell'south law of refraction using the principle of least time. Information technology involves differential calculus, so if you aren't comfortable with that nonetheless, don't fright. Just utilize the law and come back to information technology when you lot can.
Here'south the setup. A beam of light of length d1 propagating through a medium with speed of light due south1 strikes a material (bluish) with a speed of light due south2 . Other dimensions necessary for the derivation are shown.

Our strategy will be to find the full time it will have to travel from a point in the first medium to a known bespeak in the second. The principle of least time always applies to optics, and it says that light volition always take a path that ensures that it travels from place to place in the shortest-possible fourth dimension. We brainstorm by rearranging the definition of speed:
$$s = \frac{d}{t} \; \longrightarrow \; t = \frac{d}{southward}$$
The two distances, d1 and d2 , can be rewritten using the Pythagorean theorem:
$$t = \frac{\sqrt{x^2 + h^two}}{s_1} + \frac{\sqrt{(a - x)^2 + y^ii}}{s_2}$$
Now we take the derivative of that expression with respect to the variable x, which we'll relate to our angles subsequently, setting the derivative to zero to find the minimum in the fourth dimension:
$$ \brainstorm{marshal} \frac{dt}{dx} &= \frac{\frac{1}{2}(x^ii + h^2)^{-i/two} \cdot 2x}{s_1} \\ \\ &+ \frac{\frac{1}{2}((a - x)2 + y^2)^{-1/ii} \cdot 2(a - x)(-1)}{s_2} = 0 \stop{align}$$
Some cancellation and rearranging gives:
$$\frac{10}{s_1\sqrt{x^2 + h^two}} + \frac{-(a - x)}{s_2\sqrt{(a - x)^2 - y^2}} = 0$$
Nosotros can add the second term to both sides to get an equality:
$$\frac{x}{s_1 \sqrt{ten^2 + h^2}} = \frac{a - 10}{s_2\sqrt{(a - 10)^ii + y^two}}$$
Now recall that
$$ \begin{align} d_1 &= \sqrt{ten^2 + h^2} \text{ and} \\ \\ d_2 &= \sqrt{(a - 10)^2 + y^2} \end{align}$$
Hold on to that for a infinitesimal and consider the sines of the angles of incidence and refraction:
$$ \begin{align} sin(\theta_i) &= \frac{ten}{\sqrt{x^2 + h^ii}} \text{ and} \\ \\ sin(\theta_r) &= \frac{a - x}{\sqrt{(a - x)^2 + y^two}} \cease{align}$$
Substituting those into our equality gives
$$\frac{sin(\theta_i)}{s_1} = \frac{sin(\theta_r)}{s_2}$$
Now if we note that the index of refraction, northward = c/s (c = speed of light in vacuum) can be rewritten to substitute for 1/s1 and 1/s2 in the last expression,
$$n = \frac{c}{s} \; \longrightarrow \; \frac{1}{due south} = \frac{northward}{c}$$
we get
$$\frac{n_1}{c} sin(\theta_i) = \frac{n_2}{c} sin(\theta_r)$$
The c'south are redundant and can be cancelled, giving Snell's law.
$$n_1 \, sin(\theta_1) = n_2 \, sin(\theta_2)$$
Like shooting fish in a barrel peasy, lemon squeezy.
Do issues
| one. | A laser beam enters the end of an optical fiber (glass fiber) at an bending of 23˚ from the normal to the stop of the fiber, as shown. Calculate the angle of refraction of the beam within the fiber if the index of refraction of the fiber is n = 1.45. |
Solution | |
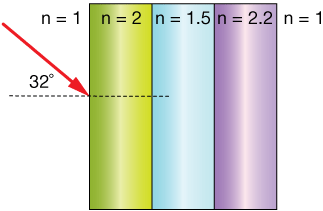
| two. | A beam of light propagating through air (n = i.00) strikes a stack of transparent materials with indices of refraction as shown in the figure at an angle of 32˚. Calculate the angles of incidence and refraction all the way through the stack and calculate the overall angle of refraction of the stack with respect to the kickoff incoming beam. |
Solution |
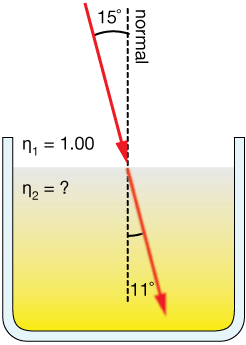
| 3. | A beam of light propagating through air (n = 1.00) strikes the surface of a liquid at a 15˚ angle. If the refracted beam makes an 11˚ angle with the surface of the liquid, calculate the index of refraction of the liquid. |
Solution | |
| iv. | A light ray moving through a rectangular slab of fabric called CR39 (n = one.498) at an angle of 49˚ enters another medium at an angle of 41˚. Summate the index of refraction of the second medium. CR39 is a plastic commonly used for eyeglasses. |
Solution |
![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website non specifically attributed to another source were created past me and I reserve all rights as to their utilize. Any opinions expressed on this website are entirely mine, and exercise not necessarily reflect the views of whatever of my employers. Please feel free to ship any questions or comments to jeff.cruzan@verizon.net.



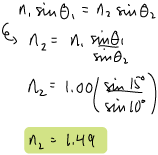

0 Response to "Light Travels Through a Substance at 1.97"
Post a Comment